6. 量化
量化理论源于论文:Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference
该论文地址:https://arxiv.org/abs/1712.05877
本章介绍TPU-MLIR的量化设计,重点在该论文在实际量化中的应用。
6.1. 基本概念
INT8量化分为非对称量化和对称量化。对称量化是非对称量化的一个特例,通常对称量化的性能会优于非对称量化,而精度上非对称量化更优。
6.1.1. 非对称量化
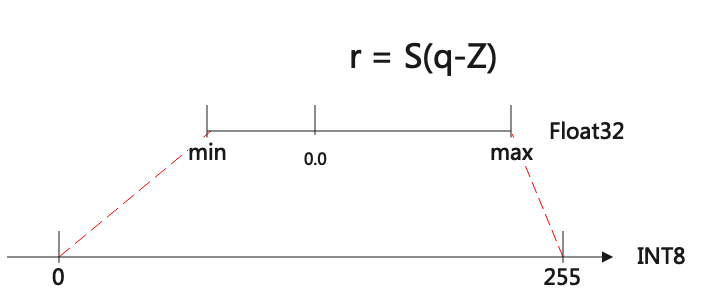
图 6.1 非对称量化
如上图所示,非对称量化其实就是把[min,max]范围内的数值定点到[-128, 127]或者[0, 255]区间。
从int8到float的量化公式表达如下:
其中r是真实的值,float类型;q是量化后的值,INT8或者UINT8类型;
S表示scale,是float;Z是zeropoint,是INT8类型;
当量化到INT8时,qmax=127,qmin=-128; UINT8时,qmax=255,qmin=0
反过来从float到int8的量化公式如下:
6.1.2. 对称量化
对称量化是非对称量化Z=0时的特例,公式表达如下:
threshold是阈值,可以理解为Tensor的范围是[-threshold, threshold]
这里 \(S = threshold / 128\),通常是activation情况;
对于weight,一般 \(S = threshold / 127\)
对于UINT8,Tensor范围是[0, threshold],此时 \(S = threshold/ 255.0\)
6.2. Scale转换
论文中的公式表达:
换个表述来说,就是浮点数Scale,可以转换成Multiplier和rshift,如下表达:
举例说明:
Multiplier支持的位数越高,就越接近Scale,但是性能会越差。一般芯片会用32位或8位的Multiplier。
6.3. 量化推导
我们可以用量化公式,对不同的OP进行量化推导,得到其对应的INT8计算方式。
对称和非对称都用在Activation上,对于权重一般只用对称量化。
6.3.1. Convolution
卷积的表示式简略为: \(Y = X_{(n,ic,ih,iw)}\times W_{(oc,ic,kh,kw)} + B_{(1,oc,1,1)}\)
代入int8量化公式,推导如下:
非对称量化特别注意的是,Pad需要填入Zx
对称量化时,Pad填入0,上述推导中Zx和Zy皆为0
在PerAxis(或称PerChannal)量化时,会取Filter的每个OC做量化,推导公式不变,但是会有OC个Multiplier、rshift
6.3.2. InnerProduct
表达式和推导方式与(Convolution)相同
6.3.3. Add
加法的表达式为: \(Y = A + B\)
代入int8量化公式,推导如下:
加法最终如何用TPU实现,与TPU具体的指令有关。
这里对称提供的方式是用INT16做中间buffer;
非对称是先反量化成float,做加法后再重量化成INT8
6.3.4. AvgPool
平均池化的表达式可以简写为: \(Y_i = \frac{\sum_{j=0}^{k_hk_w}{(X_j)}}{k_h*k_w}\)
代入int8量化公式,推导如下:
这里Multiplier可以用32位,也可以用8位;对于对称量化,Zx和Zy为0